HISTORIA DE LAS ECUACIONES:


El origen y la solución de las ecuaciones de segundo grado son de gran antigüedad. En Babilonia se conocieron algoritmospara resolverla. Fue encontrado independientemente en otros lugares del mundo. En Grecia, el matemático Diofanto de Alejandría aportó un procedimiento para resolver este tipo de ecuaciones (aunque su método sólo proporcionaba una de las soluciones, incluso en el caso de que las dos soluciones sean positivas). La primera solución completa la desarrolló el matemático Al-Juarismi (o Al-Khwarizmi según otras grafías), en el siglo IX en su trabajo Compendio de cálculo por reintegración y comparación, cerrando con ello un problema que se había perseguido durante siglos. Basándose en el trabajo de Al-Juarismi, el matemático judeoespañol Abraham bar Hiyya, en su Liber embadorum, discute la solución de estas ecuaciones.[cita requerida] Hay que esperar a Évariste Galois para conseguir resolver en general las ecuaciones polinómicas, o saber cuándo son irresolubles por radicales, que viene a ser una generalización de los métodos de resolución de las ecuaciones de segundo grado.
La primera gran dificultad que surgió en la solución de ecuaciones cuadráticas se dio con la ecuación 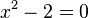en la época de los pitagóricos, al calcular la longitud de la diagonal de un cuadrado de lado 1.No se podía expresar la raíz cuadrada de dos como razón de dos números enteros. 9 . Lo que permitió la formulación de números irracionales.
Luego , ya en el Renacimiento, al resolver 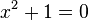, pues exige hallar un número real cuyo cuadrado sea -1; y se sabe que el cuadrado de cualquier real es positivo; lo que se superó con la adopción de números imaginarios y la definición de la unidad imaginaria i que cumple























Muhammad ibn Musa al-Jwarizmi

(Muhammad o Muhammed ibn Musa al-Khwarizmi, al-Juarismi o al-Jwarizmi; ?-?, c. 850) Matemático árabe. Escribió una obra titulada Libro de la reducción, cuya versión latina tuvo gran influencia en la matemática europea hasta mediados del siglo XV. En ella indicó las primeras reglas del cálculo algebraico: la transposición de los términos de uno a otro miembro de una ecuación, previo cambio de signo, y la anulación de términos idénticos en ambos miembros. También estudió las ecuaciones de segundo grado y otras cuestiones matemáticas. La latinización de su nombre dio lugar a la palabra «guarismo».





Poco sabemos acerca de la vida de este astrónomo, geógrafo y matemático musulmán del siglo IX. Era natural de Juwarizm (Jhiva), y residió en el Irak, en la corte del califa abasida al-Namùn (813-833). Figuró entre los familiares de este soberano, muy aficionado a las ciencias exactas; participó en la medición de la declinación solar, llevada a cabo en el curso de aquel reinado, y murió hacia el año 850.

Con su Kitab al-yabr wa-l-muqabala o Libro del álgebra (literalmente, Libro de la reducción, o bien "de la integración" o "compensación"), al-Jwarizmi inició la literatura matemática de los musulmanes. Traducido al latín por Rodolfo Chester y Gherardo da Cremona (en el siglo XII), ejerció grandísima influencia en los matemáticos europeos hasta el siglo XV. Con esta obra de al-Jwarizmi, el álgebra penetra por primera vez en el mundo musulmán, después de haber recorrido un largo camino que desde Babilonia la había llevado a la India y a Grecia.

De la popularidad de este libro dan prueba dos términos de nuestro más común lenguaje matemático. En primer lugar, la palabra "algoritmo", que hoy, después de haber pasado por varios significados, indica un "procedimiento constante de cálculo" y que deriva evidentemente del nombre de al-Jwarizmi (igualmente la palabra "guarismo"). Y en segundo lugar, la misma palabra "álgebra", introducida en Occidente por medio de este tratado árabe, en el que el término "al-yéber" designa la conocida operación por la que un término pasa de un miembro a otro de una ecuación, cambiando de signo. En realidad, esa palabra tiene su raíz más antigua en la forma babilónica "gabru-inaliaru" que significa "parangonar", "confrontar", "poner en ecuación







El álgebra de al-Jwarizmi no emplea todavía abreviaciones simbólicas como la nuestra (este progreso no llegará hasta el siglo XVII, esto es, después del Renacimiento), sino que está escrita con todas las palabras, como un tratado de ciencias naturales ("álgebra retórica"). No existe siquiera un símbolo para indicar la incógnita, la cual es designada siempre con el término de "say", de donde procede nuestro "cosa", que durante tantos siglos (hasta principios de la Edad Moderna) tuvo curso en toda Europa, al igual que los términos "cosista" (por algebrista) y "cosística" (por álgebra).

En la obra de al-Jwarizmi se estudian no sólo las ecuaciones de primer grado, sino también las de segundo (por ejemplo: x2 + 10x - 39 = 0), con un método que substancialmente no difiere del actual. Las ecuaciones de primer grado cuyas soluciones han de estar en números enteros (porque se refieren a problemas que admiten sólo tales soluciones, como, por ejemplo, cuando se busca un número de hombres, o de caballos, etc.) son tratados con el método de "falsa suposición" o, como se dice comúnmente, "falsa posición". Es evidente la influencia que los matemáticos griegos ejercieron en la formación de este tratado, especialmente en su parte geométrica; así, la demostración del teorema de Pitágoras para el caso particular del triángulo rectángulo isósceles recuerda la del Menán platónico; y el valor π (pi) = 22/7 usado a menudo por al-Jwarizmi es el descubierto por Arquímedes.

Poseemos un manuscrito en la Biblioteca Universitaria de Oxford que reproduce el original del álgebra de al-Jwarizmi, y que se remonta a 1342. En un manuscrito recientemente examinado por D. E. Smith, la conjunción "et" usada en lugar de "+" se asemeja tanto a este signo que hace pensar que deriva precisamente de ese término latino. Del mismo autor tiene también mucha importancia un escrito conocido sólo en versión latina, Algoritmi de numero Indorum, que proporciona las más antiguas informaciones acerca del uso que hacían los árabes del sistema de numeración de base décima (o indio), hoy usado comúnmente en todo el mundo civilizado.